Neuartige Bildaufnahmesysteme
Neuartige Bildaufnahmesysteme
Bevor Bilder und Videos verarbeitet und analysiert werden können, muss in einem ersten Schritt das erforderliche Material aufgezeichnet bzw. verbessert oder rekonstruiert werden. Dazu sind im ersten Abschnitt die Themen am Lehrstuhl zur Bildaufnahme gesammelt, insbesondere die Aufnahme und Verarbeitung multispektraler Daten und die Aufnahme mit Mehrkamerasystemen. Durch die Messung von spektralen Komponenten, z.B. UV oder IR, lassen sich für das menschliche Auge verborgene Informationen sichtbar machen. Kommen bei der Aufnahme von Bildern und Videos mehrere Kameras zum Einsatz, so lassen sich stereoskopische Anwendungen entwickeln.
Im dritten Abschnitt wird die Bildrekonstruktion näher betrachtet. Dabei wird zum Einen ein neuartiges Sensorkonzept (unregelmäßige Abtastung) und zum Anderen die Umtastung von Bildern erläutert.
Zum Abschluss wird im letzten Abschnitt das Augenmerk auf die Bildverbesserung gelegt. Dort ist insbesondere die Verschleierung und Rekonstruktion von fehlenden Bildbereichen gezeigt.
Bildaufnahme
Hyperspektrale Bildgebung
| Ihr Ansprechpartner |
| Frank Sippel, M.Sc. |
| E-Mail: frank.sippel@fau.de |
| Link zur Person |
| PD Dr.-Ing. habil. Jürgen Seiler |
| E-Mail: juergen.seiler@fau.de |
| Link zur Person |
Die Aufnahme hyperspektraler Bilddaten gewinnt zunehmend für Anwendungen in der Bild- und Videosignalverarbeitung an Bedeutung. So werden zum Beispiel in modernen biometrischen Sicherheitssystemen hyperspektrale Aufnahmen verwendet, um die Identität von Personen zu prüfen. Auch in der Landwirtschaft und in der Medizin werden laufend neue Ansätze veröffentlicht, bei denen zum Beispiel durch hyperspektrale Bildaufnahmen der Gesundheitszustand von Pflanzen und Menschen erfasst werden kann.
Am Lehrstuhl beschäftigen wir uns unter anderem mit innovativen Systemen zur Aufnahme von hyperspektralen Bildern und Videos. Außerdem wird die Rekonstruktion von hyperspektralen Daten und deren effiziente Codierung näher erforscht. Die folgenden Aufnahmen zeigen welche Informationen mit Hilfe hyperspektraler Aufnahmen sichtbar gemacht werden können (für vergrößerte Ansicht bitte Bilder anklicken). Das Aufnahmesystem und die zugehörigen Algorithmen wurden am Lehrstuhl entwickelt.
 |
 |
 |
Spektrale Rekonstruktion
| Ihr Ansprechpartner |
| Frank Sippel, M.Sc. |
| E-Mail: frank.sippel@fau.de |
| Link zur Person |
| PD Dr.-Ing. habil. Jürgen Seiler |
| E-Mail: juergen.seiler@fau.de |
| Link zur Person |
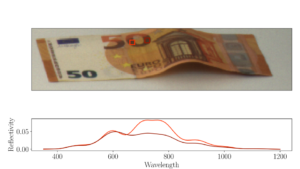
Die Benutzung von multi- und hyperspektalen Aufnahmesystemen (siehe oben) führt zu weiteren Herausforderungen. Für eine Vielzahl and Anwendungen sind die reflektierten Spektren essenzielle Informationen, um klassifizieren zu können. Demnach ist die Rekonstruktion der emittierten Spektren aus multispektralen Aufnahmen eine fundamentale Berechnung. Diese Berechnung beinhaltet diverse Fragestellungen. Üblicherweise werden mehr Variablen rekonstruiert als Beobachtungen zur Verfügung stehen. Um das zu lösen, muss man Vorkenntnisse über Spektren einarbeiten. Außerdem sind multispektrale Videos, z.B. stelle man sich eine Drohne, die über Felder fliegt und die Gesundheit von Pflanzen misst, vor, typischerweise stark verrauscht, da jedes einzelne Bild nur eine begrenzte Belichtungszeit hat. Dementsprechend müssen spektrale Rekonstruktionstechniken entwickelt werden, die robust gegenüber verrauschten Bildern arbeiten. Die Anwendungen von so einer Technik sind extrem vielseitig. Zum Beispiel können verschiedene Plastikarten unterschieden werden, Medikamentenfälschungen erkannt werden, oder Sicherheitsmerkmale auf Geldscheinen analysiert werden:
| Rekonstruierte Spektren (die Farbe der Marker entspricht der Farbe der Spektren) | Rekonstruierte Bilder an bestimmten Wellenlängen |
 |
 |
Bildrekonstruktion
Rekonstruktion unregelmäßig abgetasteter Daten
| Ihr Ansprechpartner |
| Teresa Stürzenhofäcker, M.Sc. |
| E-Mail: teresa.stuerzenhofaecker@fau.de |
| Link zur Person |
| PD Dr.-Ing. habil. Jürgen Seiler |
| E-Mail: juergen.seiler@fau.de |
| Link zur Person |
Mit Hilfe der Frequenzselektiven Rekonstruktion (FSR) können Bilder anhand von wenigen, unregelmäßig abgetasteten Bildpunkten rekonstruiert werden. Hierbei handelt es sich um ein Problem des Compressed Sensing. Gegenüber regelmäßiger Abtastung kommt es zu einem reduzierten Aliasing, wodurch nach geeigneter Rekonstruktion eine höhere Bildqualität möglich ist.
Eine mögliche Anwendung der unregelmäßigen Abtastung ist das sogenannte 1/4-Sampling. Hierbei wird ein Kamerasensor mit regelmäßig angeordneten Pixeln teilweise maskiert, so dass ein unregelmäßiges Abtastmuster entsteht. Unter Verwendung einer dünn besetzen Repräsentation kann mit Hilfe der FSR ein hochaufgelöstes Bild rekonstruiert werden.

Beispiel für die Rekonstruktion unregelmäßig abgetasteter Bilddaten beim 1/4-Sampling
Um die Leistungsfähigkeit der Frequenzselektiven Rekonstruktion auch einmal selbst testen zu können stellen wir den Algorithmus hier als Gitlab Projekt zur Verfügung.
Bildumtastung
| Ihre Ansprechpartnerin |
| Viktoria Heimann, M.Sc. |
| E-Mail: viktoria.heimann@fau.de |
| Link zur Person |
Digitale Bilder können als reguläre zweidimensionale Gitter angenommen werden. Wird ein digitales Bild nun in irgendeiner Weise transformiert, so werden die Bildpunkte auf beliebige Koordinatenpositionen verschoben. Dies bedeutet, dass die Punkte weder effizient in einer Matrix gespeichert werden können, noch ist es möglich Bilpunkte an nicht ganzzahligen Positionen auf einem digitalen Bildschirm anzusehen. Um diese Probleme zu lösen, müssen an beliebigen Stellen liegende Bildpunkte auf ein Gitter an ganzzahligen Koordinaten interpoliert werden. Wir verwenden hierfür die frequenzselektive Bildumtastung. Wie bei der oben bereits erläuterten frequenzselektiven Rekonstruktion, wird hier ebenfalls ausgenutzt, dass Bilder im Frequenzbereich dünnbesetzt sind. Durch Wahl und Überlagerung geeigneter Basisfunktionen kann dann das Bild an beliebigen Stellen rekonstruiert werden und so auf einem digitalen Bildschirm dargestellt werden. Mögliche Anwendungen für die frequenzselektive Bildumtastung sind beispielsweise affine und projektive Abbildungen, wie die unten gezeigte Bildrotation, aber auch örtliche und zeitliche Auflösungserhöhungen, Super-Resolution und Frame-Rate Up-Conversion und viele weitere mehr.
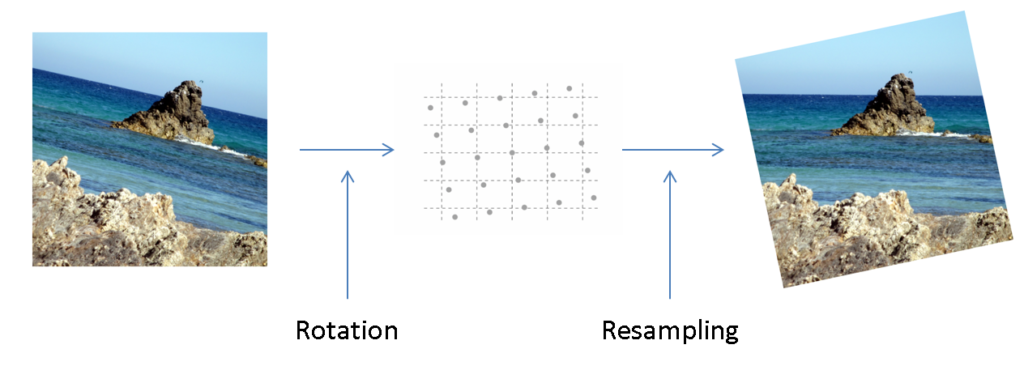
Bildverbesserung
Fehlerverschleierung von Bilddaten
| Ihre Ansprechpartner |
| Nils Genser, M.Sc. |
| E-Mail: nils.genser@fau.de |
| Link zur Person |
| PD Dr.-Ing. habil. Jürgen Seiler |
| E-Mail: juergen.seiler@fau.de |
| Link zur Person |
Bei der Übertragung von Bildern und Videos per Mobilfunk oder über das Internet besteht die Gefahr, dass Übertragungsfehler auftreten. Diese äußern sich in den Bildern oder Videosequenzen darin, dass einzelne Bildbereiche nicht korrekt decodiert und dargestellt werden können. Es ist aber möglich, diese verloren gegangenen Bildbereiche ausgehend von korrekt empfangenen Bildbereichen zu rekonstruieren. Hierzu wurde am Lehrstuhl die Selektive Extrapolation entwickelt. Dieses Verfahren ist in der Lage, beliebige Bildinhalte zu rekonstruieren und kann sowohl auf Bilder als auch auf Videosequenzen angewendet werden.
Beispiele für die Verschleierung von gestörten Bilddaten
| Originalbild | Gestörtes Bild | Verschleiertes Bild |
 |
 |
 |
Bildrestauration durch Selektive Extrapolation
Neben der Verschleierung von Störungen, die durch Übertragungsfehler entstanden sind, kann die Selektive Extrapolation auch zur Bildrestauration verwendet werden. Dabei werden Beschädigungen oder störende Objekte aus Bildern entfernt. Um dies zu erreichen, müssen in einem ersten Schritt manuell die zu extrapolierenden Bereiche gekennzeichnet werden. Dazu wird eine Binärmaske, in der alle zu ersetzenden Bereiche gleich Null sind benötigt. Anschließend wird das Bild in Blöcke aufgeteilt und auf all den Blöcken, die zu extrapolierende Bereiche enthalten die 2D Selektive Extrapolation durchgeführt.
Zwei Beispiele für die Restauration von Bildern durch Selektive Extrapolation:
 |
 |
Um die Leistungsfähigkeit der Selektiven Extrapolation auch einmal selbst testen zu können stellen wir den Algorithmus hier als Gitlab Projekt zur Verfügung.
2023
- , , , :
Image Super-Resolution Using T-Tetromino Pixels
Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)
BibTeX: Download - , , , :
Improving Spherical Image Resampling through Viewport-Adaptivity
IEEE International Conference on Image Processing (ICIP) (Kuala Lumpur, 8. Oktober 2023 - 11. Oktober 2023)
DOI: 10.1109/ICIP49359.2023.10222645
URL: https://arxiv.org/abs/2306.13692
BibTeX: Download
2022
- , , :
Frequency-Selective Geometry Upsampling of Point Clouds
IEEE International Conference on Image Processing (ICIP) 2022 (Bordeaux, 16. Oktober 2022 - 19. Oktober 2022)
DOI: 10.1109/ICIP46576.2022.9897920
URL: https://arxiv.org/abs/2205.01458
BibTeX: Download - , , :
Resampling and Reconstructing Corrupted Images for Image Classification
IEEE International Workshop on Multimedia Signal Processing (Shanghai (virtually), 26. September 2022 - 28. September 2022)
URL: https://arxiv.org/abs/2210.15444
BibTeX: Download
2021
- , , :
A Novel End-To-End Network for Reconstruction of Non-Regularly Sampled Image Data Using Locally Fully Connected Layers
23rd International Workshop on Multimedia Signal Processing (MMSP) (Tampere, Finland, 6. Oktober 2021 - 8. Oktober 2021)
DOI: 10.1109/MMSP53017.2021.9733541
BibTeX: Download - , , :
Novel Consistency Check for Fast Recursive Reconstruction of Non-Regularly Sampled Video Data
IEEE International Conference on Image Processing (ICIP) (Anchorage, 19. September 2021 - 22. September 2021)
DOI: 10.1109/icip42928.2021.9506567
BibTeX: Download - , , :
Frame Rate Up-Conversion Using Key Point Agnostic Frequency-Selective Mesh-to-Grid Resampling
IEEE International Conference on Acoustics, Speech and Signal Processing (Toronto (Virtual Conference), 6. Juni 2021 - 11. Juni 2021)
DOI: 10.1109/ICASSP39728.2021.9413684
URL: https://arxiv.org/abs/2210.10444
BibTeX: Download - , , :
Spatio-spectral Image Reconstruction Using Non-local Filtering
2021 IEEE International Conference on Visual Communications and Image Processing (VCIP) (München, 5. Dezember 2021 - 8. Dezember 2021)
DOI: 10.1109/VCIP53242.2021.9675421
URL: https://arxiv.org/pdf/2209.07890.pdf
BibTeX: Download - , , :
Hyperspectral Image Reconstruction from Multispectral Images Using Non-Local Filtering
23rd International Workshop on Multimedia Signal Processing (Tampere, 6. Oktober 2021 - 8. Oktober 2021)
DOI: 10.1109/MMSP53017.2021.9733655
URL: https://arxiv.org/pdf/2209.07891.pdf
BibTeX: Download
2020
- , , , , :
Enhanced Image Reconstruction From Quarter Sampling Measurements Using an Adapted Very Deep Super Resolution Network
IEEE International Conference on Image Processing (ICIP) (Abu Dhabi (Virtual Conference), 25. Oktober 2020 - 28. Oktober 2020)
DOI: 10.1109/icip40778.2020.9191047
BibTeX: Download - , , , :
Dynamic Image Sampling Using a Novel Variance Based Probability Mass Function
In: IEEE Transactions on Computational Imaging 6 (2020), S. 1440-1450
ISSN: 2333-9403
DOI: 10.1109/TCI.2020.3031077
BibTeX: Download - , , , :
Boosting Compressed Sensing Using Local Measurements and Sliding Window Reconstruction
In: IEEE Transactions on Image Processing 29 (2020), S. 7931 - 7944
ISSN: 1057-7149
DOI: 10.1109/TIP.2020.3007822
BibTeX: Download - , , :
Key Point Agnostic Frequency-Selective Mesh-to-Grid Image Resampling using Spectral Weighting
IEEE International Workshop on Multimedia Signal Processing (MMSP) (Tampere (Virtual Conference), 21. September 2020 - 24. September 2020)
DOI: 10.1109/MMSP48831.2020.9287096
URL: https://arxiv.org/abs/2203.08086
BibTeX: Download - , , , :
Real-Time Frequency Selective Reconstruction through Register-Based Argmax Calculation
IEEE International Workshop on Multimedia Signal Processing (MMSP) (Tampere, 21. September 2020 - 24. September 2020)
DOI: 10.1109/MMSP48831.2020.9287071
URL: https://arxiv.org/abs/2202.13926
BibTeX: Download - , , , :
Structure-preserving spectral reflectance estimation using guided filtering
In: Journal of the Optical Society of America A-Optics Image Science and Vision 37 (2020), S. 1695-1710
ISSN: 1084-7529
DOI: 10.1364/JOSAA.400485
URL: https://arxiv.org/pdf/2209.07889.pdf
BibTeX: Download
2019
- , , :
Joint Regression Modeling and Sparse Spatial Refinement for High-Quality Reconstruction of Distorted Color Images
IEEE International Conference on Image Processing (ICIP) (Taipei, 22. September 2019 - 25. September 2019)
DOI: 10.1109/icip.2019.8803567
BibTeX: Download - , , , :
A Python-based Laboratory Course for Image and Video Signal Processing on Embedded Systems
In: Heliyon 5 (2019)
ISSN: 2405-8440
DOI: 10.1016/j.heliyon.2019.e02560
BibTeX: Download - , , , , , :
Toward Bridging the Simulated-to-Real Gap: Benchmarking Super-Resolution on Real Data
In: IEEE Transactions on Pattern Analysis and Machine Intelligence 41 (2019)
ISSN: 0162-8828
DOI: 10.1109/TPAMI.2019.2917037
URL: https://www5.informatik.uni-erlangen.de/Forschung/Publikationen/2019/Koehler19-TBT.pdf
BibTeX: Download - , , , :
Motion-Adapted Three-Dimensional Frequency Selective Extrapolation
IEEE International Conference on Acoustics, Speech, and Signal Processing (Brighton, UK, 12. Mai 2019 - 17. Mai 2019)
In: IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 2019
DOI: 10.1109/ICASSP.2019.8683218
BibTeX: Download
2018
- , , :
Motion Estimation for Fisheye Video with an Application to Temporal Resolution Enhancement
In: IEEE Transactions on Circuits and Systems For Video Technology (2018), S. 1-15
ISSN: 1051-8215
DOI: 10.1109/TCSVT.2018.2869546
BibTeX: Download - , , , :
Sparse Hartley Modeling for Fast Image Extrapolation
IEEE 20th International Workshop on Multimedia Signal Processing (MMSP) (Vancouver, 29. August 2018 - 31. August 2018)
DOI: 10.1109/MMSP.2018.8547100
BibTeX: Download - , , , :
Signal and Loss Geometry Aware Frequency Selective Extrapolation for Error Concealment
Picture Coding Symposium (PCS) (San Francisco, CA, 24. Juni 2018 - 27. Juni 2018)
DOI: 10.1109/pcs.2018.8456259
BibTeX: Download - , , :
Design Techniques for Incremental Non-Regular Image Sampling Patterns
IEEE International Conference on Imaging Systems and Techniques (IST) (Kraków, 16. Oktober 2018 - 18. Oktober 2018)
DOI: 10.1109/IST.2018.8577090
BibTeX: Download - , , :
Iterative Optimization of Quarter Sampling Masks for Non-Regular Sampling Sensors
25th IEEE International Conference on Image Processing (ICIP) (Athens, 7. Oktober 2018 - 10. Oktober 2018)
DOI: 10.1109/ICIP.2018.8451658
BibTeX: Download - , , , , , :
Dynamic Non-Regular Sampling Sensor Using Frequency Selective Reconstruction
In: IEEE Transactions on Circuits and Systems For Video Technology (2018)
ISSN: 1051-8215
DOI: 10.1109/tcsvt.2018.2876653
BibTeX: Download - , , , :
Color Channel Reconstruction for Multi-Color Multi-View Images Using Disparity and Color Similarity-based Local Linear Regression
IS&T Electronic Imaging - Image Sensors and Imaging Systems Conference (San Francisco, 28. Januar 2018 - 1. Februar 2018)
DOI: 10.2352/issn.2470-1173.2018.11.imse-292
BibTeX: Download - , , , :
Increasing Imaging Resolution by Non-Regular Sampling and Joint Sparse Deconvolution and Extrapolation
In: IEEE Transactions on Circuits and Systems For Video Technology 29 (2018), S. 308-322
ISSN: 1051-8215
DOI: 10.1109/TCSVT.2018.2796725
URL: https://arxiv.org/abs/2204.12867
BibTeX: Download - , , , :
Online decomposition of compressive streaming data using n-l1 cluster-weighted minimization
Data Compression Conference (Snowbird, Utah)
DOI: 10.1109/dcc.2018.00014
BibTeX: Download - , , , :
Compressive online decomposition of dynamic signals via n-l1 minimization with clustered priors
IEEE Statistical Signal Processing Workshop (Freiburg)
DOI: 10.1109/ssp.2018.8450742
BibTeX: Download - , , , , :
Sparse Signal Recovery with Multiple Prior Information: Algorithm and Measurement Bounds
In: Signal Processing 152 (2018), S. 417-428
ISSN: 0165-1684
DOI: 10.1016/j.sigpro.2018.06.019
URL: https://www.sciencedirect.com/science/article/pii/S0165168418302160
BibTeX: Download - , , , , :
Compressive Online Robust Principal Component Analysis via n - ℓ1 Minimization
In: IEEE Transactions on Image Processing 27 (2018), S. 4314-4329
ISSN: 1057-7149
DOI: 10.1109/TIP.2018.2831915
BibTeX: Download
2017
- , , , :
Motion Compensated Frame Rate Up-Conversion Using 3D Frequency Selective Extrapolation and a Multi-Layer Consistency Check
IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (New Orleans, LA, 5. März 2017 - 9. März 2017)
DOI: 10.1109/ICASSP.2017.7952397
BibTeX: Download - , , :
Disparity Estimation for Fisheye Images with an Application to Intermediate View Synthesis
IEEE International Workshop on Multimedia Signal Processing (MMSP) (London-Luton, UK, 16. Oktober 2017 - 18. Oktober 2017)
In: IEEE International Workshop on Multimedia Signal Processing (MMSP) 2017
DOI: 10.1109/MMSP.2017.8122251
BibTeX: Download - , , , :
Demonstration of Rapid Frequency Selective Reconstruction for Image Resolution Enhancement
IEEE International Conference on Image Processing (ICIP) (Beijing, 17. September 2017 - 20. September 2017)
DOI: 10.1109/ICIP.2017.8297158
BibTeX: Download - , , :
Local Statistics Estimation For Rapid Frequency Selective Extrapolation
International Conference on Systems, Signals and Image Processing (IWSSIP) (Poznań, 22. Mai 2017 - 24. Mai 2017)
DOI: 10.1109/IWSSIP.2017.7965575
BibTeX: Download - , , :
Scaled Fixed-Point Frequency Selective Extrapolation for Fast Image Error Concealment
IEEE International Conference on Image Processing (ICIP) (Beijing, 17. September 2017 - 20. September 2017)
DOI: 10.1109/ICIP.2017.8296649
BibTeX: Download - , , :
Iterative Denoising-Based Mesh-to-Grid Reconstruction with Hyperparametric Adaptation
IEEE International Workshop on Multimedia Signal Processing (London-Luton, 16. Oktober 2017 - 18. Oktober 2017)
DOI: 10.1109/MMSP.2017.8122288
BibTeX: Download - , , :
Frequency Selective Mesh-to-Grid Resampling for Image Communication
In: IEEE Transactions on Multimedia 19 (2017), S. 1689-1701
ISSN: 1520-9210
DOI: 10.1109/TMM.2017.2683267
BibTeX: Download - , , , :
Scalable Kernel-Based Minimum Mean Square Error Estimator for Accelerated Image Error Concealment
In: IEEE Transactions on Broadcasting 63 (2017), S. 59-70
ISSN: 0018-9316
DOI: 10.1109/TBC.2016.2619581
BibTeX: Download - , :
Super-resolution for differently exposed mixed-resolution multi-view images adapted by a histogram matching method
IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (New Orleans, LA, 5. März 2017 - 9. März 2017)
DOI: 10.1109/ICASSP.2017.7952511
BibTeX: Download - , , , , , , , :
Sequential Polarization Imaging Using Multi-View Fusion
IEEE International Workshop on Signal Processing Systems (SiPS) (Lorient, 3. Oktober 2017 - 5. Oktober 2017)
DOI: 10.1109/SiPS.2017.8110019
BibTeX: Download - , , , , :
RFVTM: A Recovery and Filtering Vertex Trichotomy Matching for Remote Sensing Image Registration
In: IEEE Transactions on Geoscience and Remote Sensing 55 (2017), S. 375-391
ISSN: 0196-2892
DOI: 10.1109/TGRS.2016.2606899
URL: http://ieeexplore.ieee.org/document/7579178/
BibTeX: Download - , , , , :
Compressive Online Robust Principal Component Analysis with Multiple Prior Information
IEEE Global Conference on Signal and Information Processing (GlobalSIP) (Montreal, 14. November 2017 - 16. November 2017)
DOI: 10.1109/GlobalSIP.2017.8309163
BibTeX: Download
2016
- , , :
Multi-Image Super-Resolution Using a Dual Weighting Scheme Based on Voronoi Tessellation
IEEE International Conference on Image Processing (ICIP) (Phoenix, AZ, 25. September 2016 - 28. September 2016)
DOI: 10.1109/ICIP.2016.7532874
BibTeX: Download - , , :
Multi-Image Super-Resolution for Fisheye Video Sequences Using Subpixel Motion Estimation Based on Calibrated Re-Projection
European Signal Processing Conference (EUSIPCO) (Budapest, 29. August 2016 - 2. September 2016)
DOI: 10.1109/EUSIPCO.2016.7760573
BibTeX: Download - , , , :
Multi-Image Super-Resolution Using a Locally Adaptive Denoising-Based Refinement
IEEE 18th International Workshop on Multimedia Signal Processing (MMSP) (Montreal, 21. September 2016 - 23. September 2016)
DOI: 10.1109/MMSP.2016.7813343
BibTeX: Download - , , , , :
Joint Shape and Centroid Adaptive Frequency Selective Extrapolation for the Reconstruction of Arbitrarily Shaped Loss Areas
Picture Coding Symposium (PCS) (Nuremberg, 4. Dezember 2016 - 7. Dezember 2016)
In: Picture Coding Symposium 2016
DOI: 10.1109/PCS.2016.7906367
BibTeX: Download - , , :
Motion Estimation for Fisheye Video Sequences Combining Perspective Projection with Camera Calibration Information
IEEE International Conference on Image Processing (Phoenix, Arizona, 24. September 2016 - 27. September 2016)
In: IEEE (Hrsg.): Proceedings of the IEEE International Conference on Image Processing 2016
DOI: 10.1109/ICIP.2016.7533210
BibTeX: Download - , :
A Data Set Providing Synthetic and Real-World Fisheye Video Sequences
IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP) (Shanghai, 20. März 2016 - 25. März 2016)
In: IEEE (Hrsg.): Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP) 2016
DOI: 10.1109/ICASSP.2016.7471935
BibTeX: Download - , , , :
Recursive Frequency Selective Reconstruction of Non-Regularly Sampled Video Data
Picture Coding Symposium (PCS) (Nuremberg, 4. Dezember 2016 - 7. Dezember 2016)
DOI: 10.1109/PCS.2016.7906325
BibTeX: Download - , , :
Texture-Dependent Frequency Selective Reconstruction of Non-Regularly Sampled Images
Picture Coding Symposium (PCS) (Nuremberg, 4. Dezember 2016 - 7. Dezember 2016)
In: Picture Coding Symposium (2016) 2016
DOI: 10.1109/PCS.2016.7906355
BibTeX: Download - , , :
Reliability-based Mesh-to-Grid Image Reconstruction
IEEE 18th Workshop on Multimedia Signal Processing (MMSP) (Montreal, 21. September 2016 - 23. September 2016)
In: IEEE Workshop on Multimedia Signal Processing (MMSP) 2016
DOI: 10.1109/MMSP.2016.7813344
BibTeX: Download - , , , :
Multi-mode kernel-based minimum mean square error estimator for accelerated image error concealment
Data Compression Conference (DCC) (Snowbird, UT, 30. März 2016 - 1. April 2016)
In: Data Compression Conference (DCC) 2016
DOI: 10.1109/DCC.2016.55
BibTeX: Download - , , , :
Robust Super-Resolution for Mixed-Resolution Multiview Image plus Depth Data
In: IEEE Transactions on Circuits and Systems For Video Technology 26 (2016), S. 814-828
ISSN: 1051-8215
DOI: 10.1109/TCSVT.2015.2426498
BibTeX: Download - , :
Adaptive Frequency Prior for Frequency Selective Reconstruction of Images from Non-Regular Subsampling
IEEE 18th Workshop on Multimedia Signal Processing (MMSP) (Montreal, 21. September 2016 - 23. September 2016)
In: IEEE Workshop on Multimedia Signal Processing (MMSP), Montreal, Canada: 2016
DOI: 10.1109/MMSP.2016.7813347
URL: https://arxiv.org/pdf/2207.06797.pdf
BibTeX: Download - , :
Distributed Parallel Image Signal Extrapolation Framework using Message Passing Interface
24th European Signal Processing Conference (EUSIPCO) (Budapest, 29. August 2016 - 2. September 2016)
In: European Signal Processing Conf. (EUSIPCO), Budapest, Ungarn: 2016
DOI: 10.1109/EUSIPCO.2016.7760214
URL: https://arxiv.org/abs/2207.00238
BibTeX: Download - , , , :
Optimized Processing Order for 3D Hole Filling in Video Sequences Using Frequency Selective Extrapolation
Picture Coding Symposium (PCS) (Nuremberg, 4. Dezember 2016 - 7. Dezember 2016)
In: Picture Coding Symposium (PCS), Nuremberg, Germany: 2016
DOI: 10.1109/PCS.2016.7906329
URL: https://arxiv.org/abs/2207.09737
BibTeX: Download - , , , , , , , :
A flexible mixed-signal image processing pipeline using 3D chip stacks
In: Journal of Real-Time Image Processing 14 (2016), S. 517-534
ISSN: 1861-8200
DOI: 10.1007/s11554-016-0628-5
BibTeX: Download - , , , :
Distributed Coding of Multiview Sparse Sources with Joint Recovery
DOI: 10.1109/PCS.2016.7906382
BibTeX: Download - , , , :
A Reconstruction Algorithm with Multiple Side Information for Distributed Compression of Sparse Sources
Data Compression Conference (Snowbird, 30. März 2016 - 1. April 2016)
In: Data Compression Conference (DCC) 2016
DOI: 10.1109/DCC.2016.95
BibTeX: Download - , , , :
Sparse Signal Reconstruction with Multiple Side Information using Adaptive Weights for Multiview Sources
IEEE International Conference on Image Processing (ICIP) (Phoenix, AZ, 25. September 2016 - 28. September 2016)
In: IEEE Int. Conf. on Image Processing (ICIP), Phoenix, AZ, USA: 2016
DOI: 10.1109/ICIP.2016.7532816
BibTeX: Download
2015
- , , , , :
Hybrid Super-Resolution Combining Example-Based Single-Image and Interpolation-Based Multi-Image Reconstruction Approaches
2015 IEEE International Conference on Image Processing (ICIP) (Quebec City, 27. September 2015 - 30. September 2015)
DOI: 10.1109/ICIP.2015.7350759
BibTeX: Download - , , , :
A Hybrid Motion Estimation Technique for Fisheye Video Sequences Based on Equisolid Re-Projection
IEEE International Conference on Image Processing (ICIP) (Québec City, 27. September 2015 - 30. September 2015)
In: Proc. of IEEE Internationl Conference on Image Processing (ICIP) 2015
DOI: 10.1109/ICIP.2015.7351468
BibTeX: Download - , , , :
Temporal Error Concealment for Fisheye Video Sequences Based on Equisolid Re-Projection
23rd European Signal Processing Conference (EUSIPCO) (Nice, 31. August 2015 - 4. September 2015)
In: Proc. of European Signal Processing Conference (EUSIPCO) 2015
DOI: 10.1109/EUSIPCO.2015.7362656
BibTeX: Download - , , , , , :
Reconstruction of Videos Taken by a Non-Regular Sampling Sensor
IEEE International Conference on Visual Communications and Image Processing (VCIP) (Singapur, 13. Dezember 2015 - 16. Dezember 2015)
DOI: 10.1109/VCIP.2015.7457801
BibTeX: Download - , , :
Denoising-based image reconstruction from pixels located at non-integer positions
IEEE International Conference on Image Processing, ICIP 2015 (Québec City, 27. September 2015 - 30. September 2015)
DOI: 10.1109/ICIP.2015.7351671
BibTeX: Download - , , :
Super-Resolution for Mixed-Resolution Multiview Images Using a Relative Frequency Response Estimation Method
IEEE International Conference on Visual Communications and Image Processing (VCIP) (Singapore, 13. Dezember 2015 - 16. Dezember 2015)
DOI: 10.1109/VCIP.2015.7457827
BibTeX: Download - , , , , :
Combining single-image and multiview super-resolution for mixed-resolution image plus depth data
23rd European Signal Processing Conference, EUSIPCO 2015 (Nice, 31. August 2015 - 4. September 2015)
DOI: 10.1109/EUSIPCO.2015.7362702
BibTeX: Download - , , , :
Super-Resolution for Mixed-Resolution Multiview Image plus Depth Data using a Novel Two-Stage High-Frequency Extrapolation Method for Occluded Areas
2015 IEEE International Conference on Image Processing (ICIP) (Quebec City, 27. September 2015 - 30. September 2015)
DOI: 10.1109/ICIP.2015.7351127
BibTeX: Download - , , , , , :
Centroid adapted frequency selective extrapolation for reconstruction of lost image areas
IEEE International Conference on Visual Communications and Image Processing (VCIP) (Singapore, 13. Dezember 2015 - 16. Dezember 2015)
DOI: 10.1109/VCIP.2015.7457805
BibTeX: Download - , , , :
Resampling Images to a Regular Grid from a Non-Regular Subset of Pixel Positions Using Frequency Selective Reconstruction
In: IEEE Transactions on Image Processing 24 (2015), S. 4540-4555
ISSN: 1057-7149
DOI: 10.1109/TIP.2015.2463084
URL: https://arxiv.org/abs/2204.12873
BibTeX: Download - , , , , , :
Concept for a CMOS Image Sensor Suited for Analog Image Pre-Processing
Friday Workshop on Heterogeneous Architectures and Design Methods for Embedded Image Systems (Grenoble, 13. März 2015 - 13. März 2015)
In: DATE Friday Workshop on Heterogeneous Architectures and Design Methods for Embedded Image Systems 2015
BibTeX: Download
2014
- , , , , :
Accelerated Hybrid Image Reconstruction for Non-Regular Sampling Color Sensors
IEEE International Conference on Visual Communications and Image Processing (VCIP) (Valletta, 7. Dezember 2014 - 10. Dezember 2014)
DOI: 10.1109/VCIP.2014.7051543
BibTeX: Download - , , , , , :
High Dynamic Range Video Reconstruction from a Stereo Camera Setup
In: Signal Processing-Image Communication 29 (2014), S. 191-202
ISSN: 0923-5965
DOI: 10.1016/j.image.2013.08.016
BibTeX: Download - , , :
Declipping of Speech Signals Using Frequency Selective Extrapolation
11. ITG Conference on Speech Communication (Erlangen, 24. September 2014 - 26. September 2014)
BibTeX: Download - , , , , :
Reconstruction of Images Taken by a Pair of Non-Regular Sampling Sensors Using Correlation Based Matching
IEEE International Conference on Image Processing (ICIP) (Paris, 27. Oktober 2014 - 30. Oktober 2014)
DOI: 10.1109/ICIP.2014.7025582
BibTeX: Download - , , , :
Reducing Randomness of Non-Regular Sampling Masks for Image Reconstruction
IEEE International Conference on Visual Communications and Image Processing (VCIP) (Valletta, 7. Dezember 2014 - 10. Dezember 2014)
DOI: 10.1109/VCIP.2014.7051555
BibTeX: Download - , , , , , , , :
Cost-effective multi-camera array for high quality video with very high dynamic range
Digital Photography X (San Francisco, CA, 2. Februar 2014 - 6. Februar 2014)
DOI: 10.1117/12.2039563
BibTeX: Download - , , , , :
An error-based recursive filling ordering for image error concealment
IEEE International Conference on Image Processing (ICIP) (Paris, 27. Oktober 2014 - 30. Oktober 2014)
DOI: 10.1109/ICIP.2014.7025509
BibTeX: Download - , , , , :
Frequency selective extrapolation with residual filtering for image error concealment
2014 IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP 2014 (Florence, 4. Mai 2014 - 9. Mai 2014)
DOI: 10.1109/ICASSP.2014.6853944
BibTeX: Download - , , , :
Reconstruction of multiview images taken with non-regular sampling sensors
2014 IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP 2014 (Florence, 4. Mai 2014 - 9. Mai 2014)
DOI: 10.1109/ICASSP.2014.6854713
BibTeX: Download
2013
- , , :
Improving block-based compensated wavelet lifting by reconstructing unconnected pixels
2013 International Symposium on Signals, Circuits and Systems, ISSCS 2013 (Iasi, 11. Juli 2013 - 12. Juli 2013)
DOI: 10.1109/ISSCS.2013.6651186
BibTeX: Download - , , , , , , , :
Evaluation of a high dynamic range video camera with non-regular sensor
SPIE Electronic Imaging - Digital Photography IX (San Francisco, 3. Februar 2013 - 7. Februar 2013)
DOI: 10.1117/12.2004258
URL: http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=1568617
BibTeX: Download - , , :
Spatio-temporal error concealment in video by denoised temporal extrapolation refinement
2013 20th IEEE International Conference on Image Processing, ICIP 2013 (Melbourne, 15. September 2013 - 18. September 2013)
DOI: 10.1109/ICIP.2013.6738332
URL: https://arxiv.org/abs/2207.03774
BibTeX: Download
2012
- , :
Multiview Super-Resolution Using High-Frequency Synthesis in Case of Temporally Subsampled Depth Information
2012 IEEE Visual Communications and Image Processing, VCIP 2012 (San Diego, CA, 27. November 2012 - 30. November 2012)
DOI: 10.1109/VCIP.2012.6410742
BibTeX: Download - , , , , :
Mixed-resolution view synthesis using non-local means refined image merging
SPIE Electronic Imaging 2012 - Stereoscopic Displays and Applications XXIII (San Francisco, 22. Januar 2012 - 26. Januar 2012)
DOI: 10.1117/12.906552
BibTeX: Download - , , , :
Robust super-resolution in a multiview setup based on refined high-frequency synthesis
2012 IEEE 14th International Workshop on Multimedia Signal Processing, MMSP 2012 (Banff, AB, 17. September 2012 - 19. September 2012)
DOI: 10.1109/MMSP.2012.6343407
BibTeX: Download - , , , , , :
Building a High Dynamic Range Video sensor with spatially non-regular optical filtering
Applications of Digital Image Processing XXXV (San Diego, CA, 12. August 2012)
DOI: 10.1117/12.928858
BibTeX: Download - , , , , :
High dynamic range video by spatially non-regular optical filtering
2012 19th IEEE International Conference on Image Processing, ICIP 2012 (Lake Buena Vista, FL, 30. September 2012 - 3. Oktober 2012)
DOI: 10.1109/ICIP.2012.6467470
BibTeX: Download - , , , :
Photometric limits for digital camera systems
In: Journal of Electronic Imaging 21 (2012), Art.Nr.: 020501
ISSN: 1560-229X
DOI: 10.1117/1.JEI.21.2.020501
BibTeX: Download - , , , , :
Defect pixel interpolation for lossy compression of camera raw data
SPIE Electronic Imaging - Visual Information Processing and Communication II (San Francisco, CA, 24. Januar 2012 - 26. Januar 2012)
DOI: 10.1117/12.907910
BibTeX: Download - , , , :
Auflösungserhöhung durch nichtregelmäßige Abtastung
In: Fachzeitschrift für Fernsehen, Film und elektronische Medien 4 (2012), S. 202-205
ISSN: 1430-9947
BibTeX: Download - , , , :
Edge modeling prediction for computed tomography images
2012 IEEE Visual Communications and Image Processing, VCIP 2012 (San Diego, California, 27. November 2012 - 30. November 2012)
DOI: 10.1109/VCIP.2012.6410795
BibTeX: Download
2011
- , , , , , , :
Color constancy and non-uniform illumination: Can existing algorithms work?
2011 IEEE International Conference on Computer Vision Workshops, ICCV Workshops 2011 (Barcelona, 6. November 2011 - 13. November 2011)
DOI: 10.1109/ICCVW.2011.6130331
BibTeX: Download - , , , , :
Moving refractive optical low-pass filter for digital cameras
SPIE Electronic Imaging - Digital Photography VII (San Francisco, CA, 24. Januar 2011 - 25. Januar 2011)
DOI: 10.1117/12.872402
BibTeX: Download - , , , :
Analysis of Processing Pipelines in Digital RAW Cameras
In: A. Heuberger, G. Elst, R. Hanke (Hrsg.): Microelectronic Systems: Circuits, Systems and Applications, Heidelberg: Springer, 2011, S. 281-293
ISBN: 978-3-642-23071-4
DOI: 10.1007/978-3-642-23071-4_27
BibTeX: Download - , , , :
Increasing camera dynamic range through in-sensor multi-exposure white balancing
2011 18th IEEE International Conference on Image Processing, ICIP 2011 (Brussels, 11. September 2011 - 14. September 2011)
DOI: 10.1109/ICIP.2011.6116340
BibTeX: Download - , , , :
Increasing imaging resolution by covering your sensor
2011 18th IEEE International Conference on Image Processing, ICIP 2011 (Brussels, 11. September 2011 - 14. September 2011)
DOI: 10.1109/ICIP.2011.6115839
BibTeX: Download - , , , , :
Sparsity-based defect pixel compensation for arbitrary camera raw images
36th IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP 2011 (Prague, 22. Mai 2011 - 27. Mai 2011)
DOI: 10.1109/ICASSP.2011.5946639
BibTeX: Download - :
Signal Extrapolation Using Sparse Representations and its Applications in Video Communication (Dissertation, 2011)
URL: http://www.dr.hut-verlag.de/9783843902373.html
BibTeX: Download - , :
Optimized and parallelized processing order for improved frequency selective signal extrapolation
19th European Signal Processing Conference, EUSIPCO 2011 (Barcelona, 30. August 2011 - 2. September 2011)
URL: https://eurasip.org/Proceedings/Eusipco/Eusipco2011/papers/1569415587.pdf
BibTeX: Download - , :
A fast algorithm for selective signal extrapolation with arbitrary basis functions
In: EURASIP Journal on Advances in Signal Processing 2011 (2011), Art.Nr.: 495394
ISSN: 1687-6172
DOI: 10.1155/2011/495394
URL: https://arxiv.org/abs/2204.14194
BibTeX: Download - , :
Motion Compensated Three-Dimensional Frequency Selective Extrapolation for improved error concealment in video communication
In: Journal of Visual Communication and Image Representation 22 (2011), S. 213-225
ISSN: 1047-3203
DOI: 10.1016/j.jvcir.2010.11.006
URL: https://arxiv.org/abs/2204.12882
BibTeX: Download - , , :
Performance evaluation of feature-based image alignment techniques for inter-sequence error concealment
2011 14th ITG Conference on Electronic Media Technology, CEMT 2011 (Dortmund, 23. März 2011 - 24. März 2010)
URL: https://www.scopus.com/inward/record.uri?partnerID=HzOxMe3b&scp=79960690775∨igin=inward
BibTeX: Download - , :
Temporal adaptation strategies for spatio-temporal image alignment in inter-sequence error concealment of digital TV
2011 18th IEEE International Conference on Image Processing, ICIP 2011 (Brussels, 11. September 2011 - 14. September 2011)
DOI: 10.1109/ICIP.2011.6116074
BibTeX: Download - , :
Difference image extrapolation for spectral completion in inter-sequence error concealment
36th IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP 2011 (Prague, 22. Mai 2011 - 27. Mai 2011)
DOI: 10.1109/ICASSP.2011.5946607
BibTeX: Download
2010
- , , :
Fixed pattern noise column drift compensation (CDC) for digital moving picture cameras
2010 17th IEEE International Conference on Image Processing, ICIP 2010 (Hong Kong, 27. September 2010 - 29. September 2010)
DOI: 10.1109/ICIP.2010.5652732
BibTeX: Download - , , , , :
Change detection in JPEG 2000 compressed video
In: Electronics Letters 46 (2010), S. 409-410
ISSN: 0013-5194
DOI: 10.1049/el.2010.2945
BibTeX: Download - , , , , :
Digital neutral density filter for moving picture cameras
Computational Imaging VIII (San Jose, CA, 17. Januar 2010 - 21. Januar 2010)
DOI: 10.1117/12.838833
BibTeX: Download - , , , :
Dynamikerweiterung durch Weißabgleich im Bildsensor
16. Farbworkshop der German Color Group (Ilmenau, 7. Oktober 2010 - 8. Oktober 2010)
In: 16. Farbworkshop der German Color Group, Ilmenau, Ilmenau: 2010
BibTeX: Download - , , , , :
Dimensioning of optical birefringent anti-alias filters for digital cameras
2010 17th IEEE International Conference on Image Processing, ICIP 2010 (Hong Kong, 26. September 2010 - 29. September 2010)
DOI: 10.1109/ICIP.2010.5651784
BibTeX: Download - , :
Content-Adaptive Motion Compensated Frequency Selective Extrapolation for error concealment in video communication
2010 17th IEEE International Conference on Image Processing, ICIP 2010 (Hong Kong, 26. September 2010 - 29. September 2010)
DOI: 10.1109/ICIP.2010.5651851
URL: https://arxiv.org/abs/2207.03770
BibTeX: Download - , :
Complex-valued frequency selective extrapolation for fast image and video signal extrapolation
In: IEEE Signal Processing Letters 17 (2010), S. 949-952
ISSN: 1070-9908
DOI: 10.1109/LSP.2010.2078504
URL: https://arxiv.org/abs/2204.14193
BibTeX: Download - , , , :
Improved mode selection in hybrid error concealment for multi-broadcast-reception
2010 IEEE International Symposium on Circuits and Systems: Nano-Bio Circuit Fabrics and Systems, ISCAS 2010 (Paris, 30. Mai 2010 - 2. Juni 2010)
In: Proceedings of 2010 IEEE International Symposium on Circuits and Systems 2010
DOI: 10.1109/ISCAS.2010.5537785
BibTeX: Download - , :
Fast and robust spatio-temporal image alignment for inter-sequence error concealment
2010 17th IEEE International Conference on Image Processing, ICIP 2010 (Hong Kong, 26. September 2010 - 29. September 2010)
DOI: 10.1109/ICIP.2010.5654241
BibTeX: Download - , , :
Spatially refined inter-sequence error concealment for a multi-broadcast receiver using frequency selective approximation
18th ACM International Conference on Multimedia ACM Multimedia 2010, MM'10 (Florence, 25. Oktober 2010 - 29. Oktober 2010)
DOI: 10.1145/1873951.1874187
BibTeX: Download
2009
- , , , :
Modeling of image shutters and motion blur in analog and digital camera systems
2009 IEEE International Conference on Image Processing, ICIP 2009 (Cairo, 7. November 2009 - 10. November 2009)
DOI: 10.1109/ICIP.2009.5413842
BibTeX: Download - , , , , :
Non-linear dark current fixed pattern noise compensation for variable frame rate moving picture cameras
17th European Signal Processing Conference, EUSIPCO 2009 (Glasgow, 24. August 2009 - 28. August 2009)
URL: https://www.scopus.com/inward/record.uri?partnerID=HzOxMe3b&scp=84863770259∨igin=inward
BibTeX: Download - , :
Multiple Selection Extrapolation for Spatial Error Concealment
2009 IEEE International Workshop on Multimedia Signal Processing, MMSP '09 (Rio De Janeiro, 5. Oktober 2009 - 7. Oktober 2009)
DOI: 10.1109/MMSP.2009.5293572
URL: https://arxiv.org/abs/2207.06795
BibTeX: Download - , , , :
Low-complexity inter-sequence error concealment based on scale-invariant feature transform
2009 IEEE International Workshop on Multimedia Signal Processing, MMSP '09 (Rio De Janeiro, 5. Oktober 2009 - 7. Oktober 2009)
DOI: 10.1109/MMSP.2009.5293321
BibTeX: Download - , , , :
Fehlerverschleierung digitaler Fernsehbildsignale bei mobilem Mehrfachempfang
ITG Fachtagung für Elektronische Medien (Dortmund, 17. März 2009 - 18. März 2009)
In: ITG Fachtagung für Elektronische Medien, Dortmund, Deutschland: 2009
BibTeX: Download - , , , :
Inter-Sequence Error Concealment for Diversity Reception of TV Sequences
17th European Signal Processing Conference, EUSIPCO 2009 (Glasgow, 24. August 2009 - 28. August 2009)
URL: https://www.scopus.com/inward/record.uri?partnerID=HzOxMe3b&scp=84863743782∨igin=inward
BibTeX: Download - , , , :
Joint Temporal and Inter-Sequence Error Concealment for Multi-Broadcast-Reception
10th Workshop Digital Broadcasting (Ilmenau, 16. September 2009 - 17. September 2009)
URL: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.150.8436&rep=rep1&type=pdf
BibTeX: Download
2008
- , , :
Histogram-based prefiltering for luminance and chrominance compensation of multiview video
In: IEEE Transactions on Circuits and Systems For Video Technology 18 (2008), S. 1258-1267
ISSN: 1051-8215
DOI: 10.1109/TCSVT.2008.926997
BibTeX: Download - , , :
4-D frequency selective extrapolation for error concealment in multi-view video
2008 IEEE 10th Workshop on Multimedia Signal Processing, MMSP 2008 (Cairns, QLD, 25. Oktober 2008 - 10. Oktober 2008)
DOI: 10.1109/MMSP.2008.4665087
BibTeX: Download - , :
Motion compensated frequency selective extrapolation for error concealment in video coding
16th European Signal Processing Conference, EUSIPCO 2008 (Lausanne, 25. August 2008 - 29. August 2008)
URL: https://www.eurasip.org/Proceedings/Eusipco/Eusipco2008/papers/1569101578.pdf
BibTeX: Download - , :
Adaptive joint spatio-temporal error concealment for video communication
2008 IEEE 10th Workshop on Multimedia Signal Processing, MMSP 2008 (Cairns, QLD, 8. Oktober 2008 - 10. Oktober 2008)
DOI: 10.1109/MMSP.2008.4665080
URL: https://arxiv.org/pdf/2207.06794.pdf
BibTeX: Download - , :
Fast orthogonality deficiency compensation for improved frequency selective image extrapolation
2008 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP (Las Vegas, NV, 31. März 2008 - 4. April 2008)
DOI: 10.1109/ICASSP.2008.4517726
URL: https://arxiv.org/abs/2207.01205
BibTeX: Download - , , , :
Image-Based Synchronization in Mobile TV for a Multi-Broadcast-Receiver
9th Workshop Digital Broadcasting (Tennenlohe, 18. September 2008 - 19. September 2008)
URL: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.142.127&rep=rep1&type=pdf
BibTeX: Download
2007
- , , :
Time-Constant Histogram Matching for Luminance and Chrominance Compensation of Multi-View Video Sequences
26th Picture Coding Symposium, PCS 2007 (Lisbon, 7. November 2007 - 9. November 2007)
URL: https://www.scopus.com/inward/record.uri?partnerID=HzOxMe3b&scp=84898069089∨igin=inward
BibTeX: Download - , :
Fading Techniques for Error Concealment in Block-Based Decoding Systems
In: IEEE Transactions on Broadcasting 53 (2007), S. 286-296
ISSN: 0018-9316
DOI: 10.1109/TBC.2006.889688
BibTeX: Download - , , :
Spatio-temporal defect pixel interpolation using 3-D frequency selective extrapolation
14th IEEE International Conference on Image Processing, ICIP 2007 (San Antonio, Texas, 16. September 2007 - 19. September 2007)
DOI: 10.1109/ICIP.2007.4379976
BibTeX: Download - , :
Spatiotemporal selective extrapolation for 3-D signals and its applications in video communications
In: IEEE Transactions on Image Processing 16 (2007), S. 2348-2360
ISSN: 1057-7149
DOI: 10.1109/TIP.2007.903261
BibTeX: Download - , , :
Orthogonality Deficiency Compensation for Improved Frequency Selective Image Extrapolation
Picture Coding Symposium (Lisbon, 7. November 2007 - 9. November 2007)
URL: http://www.eurasip.org/Proceedings/Ext/PCS2007/defevent/papers/cr1064.pdf
BibTeX: Download
2006
- , :
Spatio-temporal fading scheme for error concealment in block-based video decoding systems
2006 IEEE International Conference on Image Processing, ICIP 2006 (Atlanta, GA, 8. November 2006 - 11. Oktober 2006)
DOI: 10.1109/ICIP.2006.312807
BibTeX: Download - , :
Spatio-bi-temporal error concealment in block-based video decoding systems
2006 IEEE 8th Workshop on Multimedia Signal Processing, MMSP 2006 (Victoria, BC, 3. Oktober 2006 - 6. Oktober 2006)
DOI: 10.1109/MMSP.2006.285317
BibTeX: Download - , :
3D-deblocking for error concealment in block-based video decoding systems
25th PCS: Picture Coding Symposium 2006, PCS2006 (Peking, 24. April 2006 - 26. April 2006)
URL: https://www.scopus.com/inward/record.uri?partnerID=HzOxMe3b&scp=34047182556∨igin=inward
BibTeX: Download - , :
2D frequency selective extrapolation for spatial error concealment in H.264/AVC video coding
2006 IEEE International Conference on Image Processing, ICIP 2006 (Atlanta, GA, 8. Oktober 2006 - 11. Oktober 2006)
DOI: 10.1109/ICIP.2006.313014
BibTeX: Download - , , :
Spatio-temporal selective extrapolation for 3-D signals applied to concealment in video communications
14th European Signal Processing Conference, EUSIPCO 2006 (Florence, 4. September 2006 - 8. September 2006)
URL: https://www.scopus.com/inward/record.uri?partnerID=HzOxMe3b&scp=84862605608&origin=inward
BibTeX: Download
2005
- , :
Signalnachverarbeitung zur Qualitätsverbesserung von mobil empfangenen analogen Videodaten
Elektronische Medien: 11. Dortmunder Fernsehseminar, ITG-Fachbericht 188
BibTeX: Download - , :
Low complexity streak noise reduction for mobile TV using line selective interpolation of field information
IEEE International Conference on Image Processing 2005, ICIP 2005 (Genova, 11. September 2005 - 14. September 2005)
DOI: 10.1109/ICIP.2005.1530394
BibTeX: Download - , :
Low complexity two classes Gauss weighting filter for noise reduction in mobile received analog TV signals
13th European Signal Processing Conference, EUSIPCO 2005 (Antalya, 4. September 2005 - 8. September 2005)
URL: https://www.scopus.com/inward/record.uri?partnerID=HzOxMe3b&scp=84863649764&origin=inward
BibTeX: Download - , , :
Frequency selective signal extrapolation with applications to error concealment in image communication
In: AEÜ - International Journal of Electronics and Communications 59 (2005), S. 147-156
ISSN: 1434-8411
DOI: 10.1016/j.aeue.2005.03.015
BibTeX: Download - , , , :
Automatische TV-Logo-Entfernung durch statistische modellbasierte Detektion und frequenzselektive Kompensation
Elektronische Medien: 11. Dortmunder Fernsehseminar, ITG-Fachbericht 188 (Dortmund, 26. September 2005 - 28. September 2005)
BibTeX: Download - , , , :
Automatic TV logo removal using statistical based logo detection and frequency selective inpainting
13th European Signal Processing Conference, EUSIPCO 2005 (Antalya, 4. September 2005 - 8. September 2005)
URL: https://www.scopus.com/inward/record.uri?partnerID=HzOxMe3b&scp=84863673242∨igin=inward
BibTeX: Download
2004
- , :
Spatial error concealment of corrupted image data using frequency selective extrapolation
IEEE International Conference on Acoustics, Speech, and Signal Processing (Montreal, Que, 17. Mai 2004 - 21. Mai 2004)
DOI: 10.1109/ICASSP.2004.1326518
BibTeX: Download - , :
Minimizing a weighted error criterion for spatial error concealment of missing image data
2004 International Conference on Image Processing, ICIP 2004 (Singapore, 24. Oktober 2004 - 27. Oktober 2004)
DOI: 10.1109/ICIP.2004.1419422
BibTeX: Download
2003
- , :
Örtliche Fehlerverschleierung von gestört empfangenen Bilddaten durch frequenzselektive Extrapolation
Elektronische Medien: 10. Dortmunder Fernsehseminar, ITG-Fachbericht 179
BibTeX: Download
2000
- :
Error Concealment for SNR Scalable Video Coding in Wireless Communication
Visual Communications and Image Processing 2000, SPIE (Perth, 20. Juni 2000 - 23. Juni 2000)
BibTeX: Download - :
Image Restoration for Frame- and Object-Based Video Coding Using an Adaptive Constrained Least Squares Approach
In: Signal Processing 80 (2000), S. 2337-2345
ISSN: 0165-1684
BibTeX: Download
1998
- , :
Coding of Segmented Images Using Shape-Independent Basis Functions
In: IEEE Transactions on Image Processing 7 (1998), S. 937-947
ISSN: 1057-7149
BibTeX: Download
1997
- , :
Shape Initialisation of 3-D objects in Videoconference Scenes
Stereoscopic Displays and Virtual Reality Systems IV, SPIE (San José, 11. Februar 1997 - 14. Februar 1997)
BibTeX: Download








